Dins del projecte d’apadrinament dels alumnes de sisè als de P5 de l’escola, es programen activitats de trobada i interacció entre els dos grups. En una d’aquestes activitats, els alumnes de sisè van preparar i donar un petit obsequi als fillols com a resultat d’una investigació sobre les propietats dels nombres.
Dita investigació s’emmarca dins de l’àmbit matemàtic en l’apartat de la programació que fa referència als divisors.
L’objectiu d’aquesta bona pràctica és el de presentar als alumnes un repte tal que propiciï l’aparició de l’aplicació de conceptes matemàtics coneguts a l’aula i que en la seva aplicació es faci ús d’altres continguts rellevants de les matemàtiques propis de La dimensió de la resolució de problemes i La dimensió connexions.
Per a ambdues dimensions es planteja la reflexió sobre la predicció de resultats, la comprovació de la diversitat de camins de resolució i la selecció del més adient, escollint recursos i eines i sabent-ne explicar i argumentar l’elecció.
Dit en altres paraules, fer aflorar un aprenentatge significatiu, real i proper en un context d’un exercici del tot funcional.
Des de l’equip de mestres volíem provocar que apareguessin recursos com les diferents estratègies de comptatge, les estratègies de càlcul mental i les propietats dels nombres divisors.
Activitat
El disseny del repte d’aula:
Bossetes de fruita seca
Hem de preparar un obsequi per als nens i nenes de p5, els nostres fillols. Els prepararem una bosseta de fruita seca per a cadascun de manera que totes siguin iguals.
Tenim una bossa plena de fruita seca i l’hem de repartir de manera justa per a tots.
Condicions:
– Hem de posar-hi el mateix nombre
d’ametlles que d’avellanes i que aquest nombre sigui el més gran possible.
– Hem de repartir el blat de moro i els trossets de coco de manera que tothom en
tingui la mateixa quantitat.
Explica tots els passos que hem hagut de fer, justifica-ho i acompanya-ho amb el càlcul que sigui necessari.
Desenvolupament de l’activitat

Material:
500 grams d’avellanes
500 grams d’ametlles
125 grams de coco (cubs de coco)
100 grams de blat de moro.
Conversa inicial per establir el punt de partida: durant aquest primer intercanvi d’impressions, els diferents grups cooperatius van pactar i van prendre les decisions dels passos a seguir per tal de realitzar l’activitat. Aquestes decisions van ser: distribuir tota la fruita seca per les diferents taules, de manera que cada grup tingués de tot i es posés a fer una tria de les millors unitats de fruita seca que fossin del tot òptimes; quan cada grup hagués comptat les quantitats que tenien, les posarien en comú en un quadre de totals; amb els totals i sabent quants fillols tenim, ja podien començar a treballar.

Es reparteix el full de la tasca per tal que els i les alumnes siguin conscients dels conceptes matemàtics que apareixen en la tasca a fer, és a dir, en les bossetes de fruita seca que regalaran als seus fillols.
Resolució del problema
a. Els grups es distribueixen els rols i les tasques: classificar la fruita seca, comptar, anotar i donar els resultat.
b. Recompte de cada tipus de fruita seca. Cada grup s’organitza la manera com comptarà la fruita seca:
– Agrupar en paquets d’igual nombre de fruita seca.
– Comptar el nombre de paquets que han sortit.

 c. Recull del recompte del treball de grup en una taula general.
c. Recull del recompte del treball de grup en una taula general.
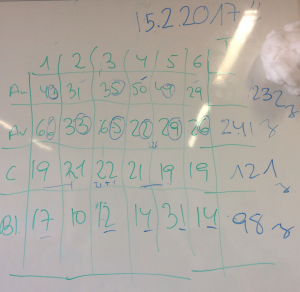
Posada en comú (quadre de totals). Un representant de cada taula transmet els totals del seu grup. Per fer el recompte general, utilitzem les estratègies de càlcul mental.
El quadre de totals queda a la pissarra.
d. Anàlisi de la taula de resultats.
S’inicia un debat d’aula per esbrinar les quantitats de fruita seca que hi ha d’haver a cada bosseta i com fer-ho segons les condicions de l’activitat.
- Descartar l’opció de divisió directa pel nombre d’alumnes i valorar fer l’estudi dels divisors dels resultats.
- Fer incís en la comprensió lectora dels enunciats remarcant els conceptes matemàtics importants que hi apareixen.
- Hem de posar-hi el mateix nombre d’ametlles que d’avellanes i que aquest nombre sigui el més gran possible.
Matemàticament estem buscant el màxim comú divisor.
| 232
ametlles |
232
[1,2,4,8,29,58,116,232] |
| 241
avellanes |
241: és un nombre primer i per tant decidim desestimar una avellana i convertir-lo en 240.
240: [1,2,3,4,5,6,8,10,12, 15,16,20,24,30,40,48,60, 80,120,240] |
Observació:
Donat que l’enunciat de l’exercici feia referència a l’m. c. d. entre ametlles i avellanes, és a dir, el nombre 8, els i les alumnes proposen canviar la condició i aprofitar les 32 ametlles i 40 avellanes sobrants per repartir-les a les bossetes. Així doncs, el nombre final d’ametlles i avellanes de cada bosseta serà de 9 malgrat que no sigui ni divisor ni comú dels totals inicials (232 i 141).
- Hem de repartir el blat de moro i els trossets de coco de manera que tothom en tingui la mateixa quantitat.
Matemàticament estem buscant els divisors.
| 121 «cubs»
de coco |
A partir de l’observació d’un alumne, afegim 4 «cubs» més per tal de facilitar el càlcul.
*Així doncs, treballem amb 125 «cubs» de coco, dels quals en posarem 5 a cada bosseta. 125 [1,5,25,125] |
| 98 grans
de blat de moro |
A partir d’una nova observació, afegim 2 grans de blat de moro més.
*Així doncs, treballem amb 100 grans de blat de moro, dels quals en posarem 4 a cada bosseta. 100 [1,2,4,5,10,20,25,50,100] |
*Emprem unitats de fruita desestimades durant la selecció de l’inici
Repartiment de la fruita seca a cada bosseta segons condicions de l’enunciat del problema.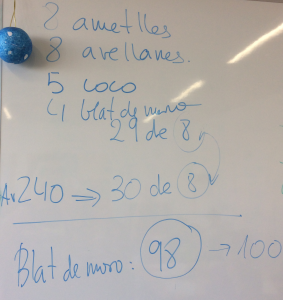
Ús de la calculadora per comprovar els càlculs i les previsions del repartiment.
Els i les alumnes cerquen tots aquells múltiples comuns entre el 232 i el 241 (240) i els divisors del 121 (125) i 98 (100).
e. Reenquadrament de la realitat a la matemàtica.
Durant l’activitat els alumnes van fent reflexions sobre el recompte real de la fruita seca per tal de facilitar el repartiment just de les bossetes.

Tal com ja hem esmentat anteriorment, a partir de les reflexions dels alumnes vam variar les quantitats de la fruita seca per facilitar-ne el repartiment. Així doncs, treballem amb 232 ametlles, 240 avellanes, ja que s’adonen que el 241 és un nombre primer, 125 «cubs» de coco (en lloc de 121) i 100 grans de blat de moro en lloc dels 98 inicials.
f. Consideracions finals.
Els i les alumnes arriben a la conclusió que dins de cada bosseta hi posarem 9 ametlles, 9 avellanes, 5 «cubs» de coco i 4 grans de blat de moro.
g. Preparació de les bossetes.
Les bossetes resultants van ser obsequiades als fillols de p5.
Per saber-ne més
Competències bàsiques de l’àmbit matemàtic: Identificació i desplegament a l’educació primària. Departament d’Ensenyament. Gener de 2013.
Decret 119/2015, de 23 de juny, d’ordenació dels ensenyaments de l’educació primària. DOGC 6900 – 26.6.2015.
Deulofeu, Jordi (2000). «Pensant en el 2001: resolució de problemes, activitat matemàtica i raonament». A PERSPECTIVA ESCOLAR, núm. 242 (febrer 2000), p. 36-43.
National Council of Teachers of Mathematics (2000). Principios y Estándares para la Educación Matemática. Sevilla: Sociedad Andaluza de Educación Matemática [traducció castellana, 2003].
JORDI ORTEGA
Mestre tutor de 6è.
Membre de la Comissió Matemàtica
MAITE RIBES
Mestra.
Membre de la Comissió Matemàtica
Escola Can Manent de Cardedeu (Vallès Oriental)



